本記事では拙著『記号論理精選問題集【述語論理】編』についてご紹介させていただきます。

記号論理の『問題集』というのは、あるようで実はありません。

それもそのはず、記号論理を資格勉強などに集中して行う人はいないからです。つまり、記号論理自体がマイナーな科目（？）という嫌いがあります。

しかし（大学の）テスト勉強などで記号論理の問題集がほしい、とおもう時もあるとおもいます。

そのために本書は出版されました。

内容紹介

既に命題論理についての問題集が同著者から出版されています。

記号論理精選問題集【命題論理】編

本記事では『記号論理精選問題集【命題論理】編』をご紹介させていただきます。本書『記号論理精選問題集【命題論理】編』は、命題論理についての純粋な問題集です。丁度、受験世界史に一問一答の問題集があるように、記号論理についても問題集あっていいんじ...

cogefra.work

その続編になります。方向性も同じです。ただ、本書では述語論理が集中的に扱われています。

述語論理の問題が50題と非常にたくさん収録されています。各設問に詳細な解説、考え方を付しました。

出典：著者紹介文（アマゾン，楽天における）

体系（公理系）としては、ゲンツェンのNK（エヌカー）が使われます。

なので、本書を使う前に同著者（管理人の私のことですが・・・）の『記号論理入門【述語論理】前編』、同『後編』を学習しておくことが望まれます。あるいは『文系のための記号論理入門ー命題論理から不完全性定理へ』でもよいでしょう。

ゲンツェン式の証明図で書かれていることに注意

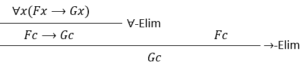
ゲンツェン式の証明図の例

本『問題集』について購入者に注意してもらいたいのは、いわゆるフィッチ式で証明はされていない、ということです。

フィッチ式の例

①　∀x(Fx→Gx)　前提より

②　Fc→Gc　①に∀-Elim

③　Fc  前提より

④　Gc  ②③に→-Elim

こういったフィッチ式ではなく、ゲンツェン式の証明図で証明（答え）が書かれています。

電子書籍

本書は電子書籍になります。

https://a.r10.to/hNwfCj

現在（2025/4/3）では楽天Kobo電子書籍ストアでのみ販売となっています（上掲リンク先）。

注意（重要性大）：本作は時期によってAmazonでのみ販売、あるいは楽天でのみ販売されていることがあります。詳しくは実際に該当ページに行って確認するか、本記事「コメント」経由でお問い合わせください。

電子書籍は現在、AmazonKindle電子書籍アプリか、楽天Kobo電子書籍アプリを使って読むのが主流になっています。

本記事はここまでになります。

本書『記号論理精選問題集【述語論理】編』について、なにかご意見ありましたら、コメント欄になにか書き込んで頂けると幸いです。