文型理系に限らず,記号論理の証明問題ができない人はびっくりする位います。本記事では,その考え方を伝えたいと思います。
真理表があれば命題論理の証明問題(いわゆる構文論)を解く必要はない、と考えるのは間違いです。なぜ間違いなのかは、それなりに論理学に精通しないとわからないことなので詳述はしません。本記事では実践を伝えたいと思います。
設問 ⊢ p→(p→(p⋁q))
以下を証明せよ。
⊢ p→(p→(p⋁q))
これは定理を表します。このレベルの記号の読み方は拙著をご参照ください。
考え方
以下のように考えてください。
① 定理なので前提はない。
② なので仮定を使わざるを得ない。
③ 仮定を使えるのは,→-Intro, ⋁-Elim, ¬-Intro.
④ 証明すべき定理の形は条件法.なので[p]1と仮定をし,→-Intro.1で締める形で証明を構想する.
⑤ まず p を前件とし,p⋁qを後件とする形で証明を組み立てる(もちろんゲンツェンのNKの証明図).
⑥ それ(⑤)ができたら「(連言で)くっつけて離す」要領で,新たに[p]2を仮定し,→-Intro.2で締める形で証明を完成させる.
以上になります。
正答は自分で書き上げてもらいたい。
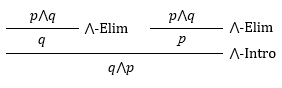 こういった証明図を自分で書き上げてください。
こういった証明図を自分で書き上げてください。
これが解答というわけではありません。
具体的な証明図は自分で書き上げてください(ゲンツェンのNKという体系)。上掲図のようになります。
本記事はここまでになります。
疑問点などありましたら、コメント欄にお願いします。




コメント(ディスカッション)