本記事では『記号論理精選問題集【命題論理】編』をご紹介させていただきます。
本書『記号論理精選問題集【命題論理】編』は、命題論理についての純粋な問題集です。
丁度、受験世界史に一問一答の問題集があるように、記号論理についても問題集あっていいんじゃないか、という考え方で作られています。
本書では命題論理の証明問題が50問と非常にたくさん収録されており、各問題に詳細な解説がついています。
文章などはKindle電子書籍リーダーというよりも、スマートフォンやPCなど普段ご使用の媒体にKindleアプリをダウンロードして読まれることを想定し構成されています(綿密なリンクと索引含む)。
出典:著者紹介文(アマゾン,楽天における)
体系(公理系)としては、ゲンツェンのNK(エヌカー)が使われます。
なので、本書を使う前に同著者の『記号論理入門【命題論理】前編』、同『後編』を学習しておくことが望まれます。
ゲンツェン式の証明図が使われていることに注意!
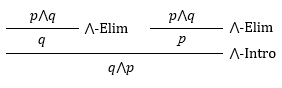 ゲンツェン式の証明図の例
ゲンツェン式の証明図の例
注意しなければならないのは、本書の解答はゲンツェン式の証明図で書かれている、ということです。
フィッチ式の解答例
① p∧q 前提
② q ①に⋀-Elim
③ p ①に⋀-Elim
④ q∧p ②③に⋀-Intro
このようなフィッチ式による証明は使われていません。
電子書籍
本書は電子書籍になります。
現在(2025/4/3)は楽天Kobo電子書籍ストアでのみ販売となっています(上掲リンク先)。
注意(重要性大):本作は時期によってAmazonでのみ販売、あるいは楽天でのみ販売されていることがあります。詳しくは実際に該当ページに行って確認するか、本記事「コメント」経由でお問い合わせください。
電子書籍は現在、AmazonKindle電子書籍アプリか、楽天Kobo電子書籍アプリを使って読むのが主流になっています。
述語論理の問題集は別
本書は命題論理に特化した『問題集』であって、述語論理の問題集を必要とする方は同著者のそれを求めることをおススメします。

本記事はここまでです。
本書『記号論理精選問題集【命題論理】編』について、なにかご意見などありましたら、コメント欄にご一筆よろしくお願いいたします。
追記:28さんへの回答
28さんの質問への回答の証明図が崩れているので、ここに再掲します。
****以下回答*****
ご質問ありがとうございます。
>私は[p]₁ [q∧r]₂ [p]₃ [q∧r]₄ と置いて1,2と3.4を別々に進めて∨‐Elimを適用しました。
いえ、恐らくそれでは上手く行かないと思います。Q4が「正しくない」という論点と同じところに落ちると思います。
つまり、
[q⋀r]2
-------⋀-Elim
[p]1 r
------∨-Intro -------∨-Intro
p∨q p∨r
-----------------------⋀-Intro
(p∨q)⋀(p∨r)
この山(糸)を2つ作る、ということだと察してますが、この最後の⋀-Introで、別々に立てたはずの仮説[p]1と[q⋀r]2をくっつけてしまってます。これは選言除去では許されないのです。論点はQ4と同じです。
もし誤解なり、腑に落ちないところがあったら、再度ご質問お願いいたします。
****回答ここまで****



コメント(ディスカッション)
本書『記号論理精選問題集【命題論理】編』について
①内容上の質問
②誤字脱字などの指摘
③リンク不全(買えない)etc.
なんでも質問等にお答えさせて頂きますので、本コメント欄にご投稿お願いします。
コメントは本コメントへの返信(ぶらさがりコメント)にしないで、新たに「スレッドを立てる」感じでお願いします。投稿者は匿名でOKです(むしろ推奨します)。投稿日時など非表示設定にしましたので、プライバシーは保てると考えています。
選言除去についてですが、相方の選言はどうでもいいので∨-introを使うところまではわかりました。しかし、∨-Elim1.2が何を意味しているかがどうしても分かりません。
ご質問ありがとうございます。
∨-Elim.1,2の論理は仮定[φ]1と[ψ]2が同時に解除されることを「1,2」で表しています。
なぜ同時に解除されるのか、というとφ⋁ψが大元にあるからです。
φ⋁ψは言える。これが∨-Elimの基本情報です。
そこからχを導き出す、というのが∨-Elimの働きです。
なので、少し誤解を招くかもしれませんが{φ⋁ψ}トχというのが∨-Elimの推論構造になります。
その推論において仮定[φ]1と[ψ]2は、あくまで踏み台であり、χを導き出すために同時に解除されなければなりません。
大体「分かれ道」の比喩で説明されることが多いです(但し、この例だと排他的選言を連想させるので、私は反対ですが、今回は便宜上採用してみます)。
① [φ]1の道を通ったらχという街に着きました。(仮定[φ]1からχが導き出された)
② [ψ]2の道を通ったらχという街に着きました。(仮定[ψ]2からχが導き出された)
この場合(①②)、[φ]1か[ψ]2いずれを選んでもχには辿り着きますよね。だから「φ⋁ψが言えればχが言える」。これが∨-Elimの推論になります。
繰り返しますが、推論として行われているのは{φ⋁ψ}トχという形です。ここを見誤らないでください。
48番の問題なのですが、解答では[p]₁ [q∧r]₂ と置いて進めて導いていましたが、私は[p]₁ [q∧r]₂ [p]₃[q∧r]₄ と置いて1,2と3.4を別々に進めて∨‐Elimを適用しました。美しさを抜きにした場合、この回答に問題はありますか?
ご質問ありがとうございます。
>私は[p]₁ [q∧r]₂ [p]₃ [q∧r]₄ と置いて1,2と3.4を別々に進めて∨‐Elimを適用しました。
いえ、恐らくそれでは上手く行かないと思います。Q4が「正しくない」という論点と同じところに落ちると思います。
つまり、
[q⋀r]2
——-⋀-Elim
[p]1 r
—-∨-Intro ——-∨-Intro
p∨q p∨r
———————–⋀-Intro
(p∨q)⋀(p∨r)
この山(糸)を2つ作る、ということだと察してますが、この最後の⋀-Introで、別々に立てたはずの仮説[p]1と[q⋀r]2をくっつけてしまってます。これは選言除去では許されないのです。論点はQ4と同じです。
もし誤解なり、腑に落ちないところがあったら、再度ご質問お願いいたします。
上掲証明図
[q⋀r]2
——-⋀-Elim
[p]1 r
—-∨-Intro ——-∨-Intro
p∨q p∨r
———————–⋀-Intro
(p∨q)⋀(p∨r)
が崩れているので、本文に書きます。