全称文についてのオイラー図とヴェン図での表現をみた。
全称文のヴェン図とオイラー図
全称文は、古い論理学（アリストテレスの三段論法を使った論理学）でも、記号論理でも、重要な位置を占める文の形式である。全称文「すべてのF はG である」∀x(Fx→Gx)この文形式について、ふつう人が直感的に持つのはオイラー図であろう。オイラ...
cogefra.work
今度は特称文での表現をみてみよう。特称文とは、次の形式を持つ文のことである。
特称文「或るF はG である」
∃x(Fx⋀Gx)
この文の形式について上手に表現しているのは、全称文の時とは正反対に、ヴェン図の方である。
ヴェン図による特称文の表現
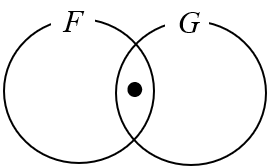
ヴェン図は、この特称文の表現において最も論理学に貢献したといえる。
重要なのは真ん中のボッチ●で、これがオイラー図になると消える。
オイラー図による特称文の表現
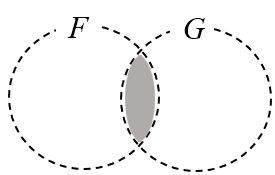
これがオイラー図での特称文の表現になる。ヴェン図と違い、塗りつぶされたところが（特称文で）主張されているところと考えられている。
破線は、不周縁(undistributed)を表している。これは古い論理学（アリストテレスの三段論法の論理学）に精通しているならわかる考え方であるが、記号論理では使わないので割愛する。
もっとも大きな違いはオイラー図では存在の主張がされていない、ということだ。
ヴェン図では●によって、それ（存在の主張）がされている。
この点において特称文に限っていえば、ヴェン図による表現の方が優れている。
以上の話についてヴェン図とオイラー図に関しては以下の記事も参照してください。
ヴェン（ベン）図とオイラー図
John Venn (1834-1923）円や丸を描いて概念や集合をイメージする、という知的作業は非常に自然な（生得的、直感的）なもので、わざわざ、それをヴェンやらオイラーに帰するのは、うなずけないところがある。しかし、それでも慣例的に、ヴ...
cogefra.work
以上の内容は古い論理学の教科書（アリストテレスの三段論法を使った論理学）に詳しく書かれています。
『論理学綱要』（内田老鶴圃，うちだろうかくほ）
John Venn (1834-1923）古い論理学（アリストテレスの三段論法を使った論理学）の代表的な教科書として岩波書店の『論理学入門』を紹介しました。もう一冊、見るだけで図書館の香りが蘇るような本として『論理学綱要』を取り上げさせても...
cogefra.work
https://cogefra.work/oldlogic/
コメント（ディスカッション）