ウィトゲンシュタインが
真理表を考えた。
かなりたくさんの人に質問される論理学の概念、空疎に真(vacuously true)について説明したいと思います。
拙著では下記のページに載っています。
文系のための記号論理入門:命題論理から不完全性定理まで §56
論理と分析:文系のための記号論理入門 p.66
条件法で前件偽
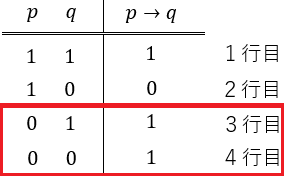
p→qの真理表
赤枠内が空疎に真を表す箇所。
空疎に真は、条件法の真理表で説明されることが多いです。
上掲画像は条件法の真理表ですが、その3行目と4行目では意味されていることは、
p→qで,p(前件)が0(偽)の時,後件 q の真偽(1か0)を問わなくても、条件法 p→q全体は有無をいわせず真になる
ということです。これが空疎に真の意味です。
どういった使われ方をするか?
以下の例はこの本のp.3に載っています。
空疎に真は、日常言語の「ならば」の意味を記号論理が汲み取っていない典型として、批判にされされることが多いのですが、その割には理系タイプの議論で大変重宝されます。
なにかいい例は・・・と考え探したのですが、以下の例がよいでしょう。すこし述語論理の知識を必要とします。
任意の集合Bに空集合は包含される:∅⊂B ・・・①
これが言えるのは空疎に真の論理からです。
包含関係⊂は、全称文として条件法を使って次のように書き換えられます。
A⊂B ←→def. ∀x(x∈A→x∈B) ・・・②
そうすると∅⊂Bは以下のように書き換えられます(←→は同値関係。論理学で文同士の間に成立するイコールみたいなもの)。
∅⊂B ←→ ∀x(x∈∅→x∈B) ・・・③
しかしx∈∅は端的に偽(空集合∅には何も属さない)。なので、条件法x∈∅→x∈B全体は空疎に真。ゆえに定義②より、∅⊂B(=①)は成立する。
空疎に真は、こんな風にして使われるのが典型です。
p→qは¬p⋁qと同値
空疎に真の舞台裏には、p→qと¬p⋁qが同値とみなされる、という論理学的常識があります。
実際の¬p⋁q真理表を書いてみれば、上掲p→qの真理表と一致するのがわかるでしょう。




コメント(ディスカッション)