円や丸を描いて概念や集合をイメージする、という知的作業は非常に自然な（生得的、直感的）なもので、わざわざ、それをヴェンやらオイラーに帰するのは、うなずけないところがある。
しかし、それでも慣例的に、ヴェン（ベン）図やオイラー図は、円や丸を描いて論理的な思考を表す手法の代表だと考えられている。
ヴェン図
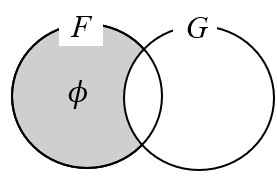
ヴェン図による全称文の表現
（この記事参照）
ヴェン図というのは上掲図のようなものをいう。
不便なことにこの２つの丸の位置は動かせない。実際、論理的思考あるいはそれに似たものを考える時、私達が使用しているのはオイラー図だといいたい。
それでもヴェン（ベン）図が歴史的に果した役割は大きいらしい。
ベン図の考案者として知られ、その成果は集合論、確率、論理学、統計学、計算機科学をはじめ、様々な分野で利用されている。
少し首をかしげたくなる叙述である。
オイラー図
オイラー図による全称文の表現
（この記事参照）
PowerPointなどを使って直感的に概念やら集合のイメージを伝える時、私達はヴェン図（ベン図）よりもオイラー図を使っている。
しかしながら、オイラー図は存在文（特称文）のイメージを伝えるのが非常に下手である。
特称文のヴェン図とオイラー図
全称文についてのオイラー図とヴェン図での表現をみた。今度は特称文での表現をみてみよう。特称文とは、次の形式を持つ文のことである。特称文「或るF はG である」∃x(Fx⋀Gx)この文の形式について上手に表現しているのは、全称文の時とは正反対...
cogefra.work
図を使って論理学を理解するのは、ほどほどに・・・
論理的な思考を図を描いて理解する、というのは素朴な意味論のかたちとしてあってもよいかも知れない。
しかしながら、私（管理人）は基本的に反対である。
どこかでその悪癖（論理的な思考を図を描いて理解すること）は止めるべきだと思っている。
図による理解は、例えば否定のところで行き詰まると思われる。
否定：図を使った論理学学習の限界
古い論理学（アリストテレスの三段論法を使った論理学）の常套手段であるヴェン図とオイラー図を使った基本文型の視覚的表現を辿って来た。古い論理学（アリストテレスの三段論法を使った論理学）には４つの基本文型がある。A: すべてのF はG である。...
cogefra.work
論理学はあくまえ記号操作の学問なので、しっかり証明図を書けるようになって学んでもらいたい。
コメント（ディスカッション）